Java二叉树的实现示例
- 2022-05-20 12:29:47
- 2928次 动力节点
1.二叉树
二叉树是一种递归数据结构,其中每个节点最多可以有 2 个子节点。
二叉树的一种常见类型是二叉搜索树,其中每个节点的值都大于或等于左子树中的节点值,并且小于或等于右子树中的节点值树。
这是这种二叉树的直观表示:
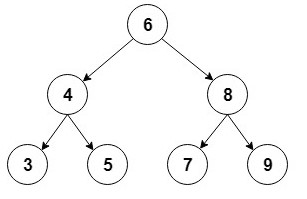
对于实现,我们将使用一个辅助Node类来存储int值,并保留对每个孩子的引用:
class Node {
int value;
Node left;
Node right;
Node(int value) {
this.value = value;
right = null;
left = null;
}
}
然后我们将添加树的起始节点,通常称为根:
public class BinaryTree {
Node root;
// ...
}
2.常用操作
现在让我们看看我们可以在二叉树上执行的最常见的操作。
(1)插入元素
我们要介绍的第一个操作是插入新节点。
首先,我们必须找到要添加新节点的位置,以保持树的排序。我们将从根节点开始遵循这些规则:
如果新节点的值小于当前节点的值,我们去左子树
如果新节点的值大于当前节点的值,我们去右子树
当当前节点为空时,我们到达了一个叶节点,我们可以在该位置插入新节点
然后我们将创建一个递归方法来进行插入:
private Node addRecursive(Node current, int value) {
if (current == null) {
return new Node(value);
}
if (value < current.value) {
current.left = addRecursive(current.left, value);
} else if (value > current.value) {
current.right = addRecursive(current.right, value);
} else {
// value already exists
return current;
}
return current;
}
接下来我们将创建从根节点开始递归的公共方法:
public void add(int value) {
root = addRecursive(root, value);
}
让我们看看如何使用此方法从我们的示例中创建树:
private BinaryTree createBinaryTree() {
BinaryTree bt = new BinaryTree();
bt.add(6);
bt.add(4);
bt.add(8);
bt.add(3);
bt.add(5);
bt.add(7);
bt.add(9);
return bt;
}
(2)寻找元素
现在让我们添加一个方法来检查树是否包含特定值。
和以前一样,我们将首先创建一个遍历树的递归方法:
private boolean containsNodeRecursive(Node current, int value) {
if (current == null) {
return false;
}
if (value == current.value) {
return true;
}
return value < current.value
? containsNodeRecursive(current.left, value)
: containsNodeRecursive(current.right, value);
}
在这里,我们通过将其与当前节点中的值进行比较来搜索该值;然后,我们将根据结果继续左或右孩子。
接下来,我们将创建从root开始的公共方法:
public boolean containsNode(int value) {
return containsNodeRecursive(root, value);
}
然后我们将创建一个简单的测试来验证树是否真的包含插入的元素:
@Test
public void givenABinaryTree_WhenAddingElements_ThenTreeContainsThoseElements() {
BinaryTree bt = createBinaryTree();
assertTrue(bt.containsNode(6));
assertTrue(bt.containsNode(4));
assertFalse(bt.containsNode(1));
}
添加的所有节点都应包含在树中。
(3)删除元素
另一种常见的操作是从树中删除一个节点。
首先,我们必须以与之前类似的方式找到要删除的节点:
private Node deleteRecursive(Node current, int value) {
if (current == null) {
return null;
}
if (value == current.value) {
// Node to delete found
// ... code to delete the node will go here
}
if (value < current.value) {
current.left = deleteRecursive(current.left, value);
return current;
}
current.right = deleteRecursive(current.right, value);
return current;
}
一旦我们找到要删除的节点,主要有 3 种不同的情况:
一个节点没有孩子——这是最简单的情况;我们只需要在它的父节点中用null替换这个节点
一个节点只有一个孩子——在父节点中,我们用它唯一的孩子替换这个节点。
一个节点有两个孩子——这是最复杂的情况,因为它需要树重组
让我们看看当节点是叶节点时如何实现第一种情况:
if (current.left == null && current.right == null) {
return null;
}
现在让我们继续讨论节点有一个孩子的情况:
if (current.right == null) {
return current.left;
}
if (current.left == null) {
return current.right;
}
在这里,我们返回非空子节点,以便将其分配给父节点。
最后,我们必须处理节点有两个孩子的情况。
首先,我们需要找到将替换已删除节点的节点。我们将使用即将被删除节点的右子树的最小节点:
private int findSmallestValue(Node root) {
return root.left == null ? root.value : findSmallestValue(root.left);
}
然后我们将最小值分配给要删除的节点,然后,我们将从右子树中删除它:
int smallestValue = findSmallestValue(current.right);
current.value = smallestValue;
current.right = deleteRecursive(current.right, smallestValue);
return current;
最后,我们将创建从根开始删除的公共方法:
public void delete(int value) {
root = deleteRecursive(root, value);
}
现在让我们检查删除是否按预期工作:
@Test
public void givenABinaryTree_WhenDeletingElements_ThenTreeDoesNotContainThoseElements() {
BinaryTree bt = createBinaryTree();
assertTrue(bt.containsNode(9));
bt.delete(9);
assertFalse(bt.containsNode(9));
}
选你想看
你适合学Java吗?4大专业测评方法
代码逻辑 吸收能力 技术学习能力 综合素质
先测评确定适合在学习
价值1998元实验班免费学













 在线咨询
在线咨询
 免费试学
免费试学