首页 > Java资讯 > 正文

Java背包问题实现

2022-04-25 10:36:38
1010次动力节点

1. 简介

背包问题是一个有很多应用的组合优化问题。在本Java教程中，动力节点小编将用 Java 解决这个问题。

2. 背包问题

在背包问题中，我们有一组物品。每个项目都有一个重量和一个价值：

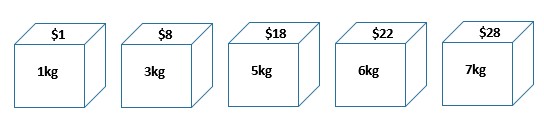
我们想把这些物品装进背包。但是，它有一个重量限制：

因此，我们需要选择总重量不超过重量限制的物品，并且它们的总价值尽可能高。例如，上面例子的最佳解决方案是选择 5kg 的物品和 6kg 的物品，在重量限制内，最大值为 40 美元。

背包问题有几种变化。在本教程中，我们将关注0-1 背包问题。在 0-1 背包问题中，每个项目要么被选中，要么被抛在后面。我们不能拿走一个项目的部分金额。此外，我们不能多次拿走一个项目。

3. 数学定义

现在让我们用数学符号形式化 0-1 背包问题。给定一组n 个项目和权重限制W，我们可以将优化问题定义为：

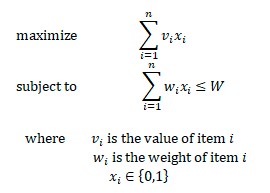
这个问题是 NP 难的。因此，目前还没有多项式时间算法来解决它。然而，有一个伪多项式时间算法使用动态规划来解决这个问题。

4. 递归解决方案

我们可以使用递归公式来解决这个问题：

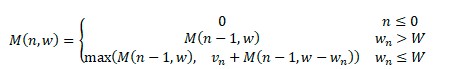
在这个公式中，M(n,w)是重量限制为w的n 个项目的最优解。它是以下两个值中的最大值：

重量限制为w的(n-1)个项目的最优解(不包括第n个项目)

第n项的值加上(n-1)项的最优解和w减去第n项(包括第n项)的权重

如果第n个项目的重量超过当前重量限制，我们不包括它。因此，属于上述两种情况的第一类。

我们可以在 Java 中实现这个递归公式：

int knapsackRec(int[] w, int[] v, int n, int W) {
    if (n <= 0) { 
        return 0; 
    } else if (w[n - 1] > W) {
        return knapsackRec(w, v, n - 1, W);
    } else {
        return Math.max(knapsackRec(w, v, n - 1, W), v[n - 1] 
          + knapsackRec(w, v, n - 1, W - w[n - 1]));
    }
}

在每个递归步骤中，我们需要评估两个次优解决方案。因此，此递归解的运行时间为O(2 n )。

5. 动态规划方案

动态规划是一种将其他呈指数级困难的规划问题线性化的策略。这个想法是存储子问题的结果，以便我们以后不必重新计算它们。

我们也可以用动态规划解决0-1背包问题。为了使用动态规划，我们首先创建一个维度从 0 到n和 0 到W的二维表。然后，我们使用自下而上的方法，用这张表计算最优解：

int knapsackDP(int[] w, int[] v, int n, int W) {
    if (n <= 0 || W <= 0) {
        return 0;
    }
    int[][] m = new int[n + 1][W + 1];
    for (int j = 0; j <= W; j++) {
        m[0][j] = 0;
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= W; j++) { 
            if (w[i - 1] > j) {
                m[i][j] = m[i - 1][j];
            } else {
                m[i][j] = Math.max(
                  m[i - 1][j], 
                  m[i - 1][j - w[i - 1]] + v[i - 1]);
            }
        }
    }
    return m[n][W];
}

在这个解决方案中，我们对项目编号n和重量限制W有一个嵌套循环。因此，它的运行时间是O(nW)。